 Odvodenie Poyntingovho vektora
Odvodenie Poyntingovho vektora
Precízny spôsob odvodenia vzťahu (11.3.3.1) vychádza zo vzorca pre objemovú hustotu energie elektromagnetického poľa (11.2.3.9). V elektromagnetickom poli si zvolíme oblasť ohraničenú uzavretou plochou S , a vypočítame energiu W nachádzajúcu sa v nej ako objemový integrál hustoty energie w :
![]()
Vypočítame deriváciu tejto energie podľa času, čím vyjadríme jej zmenu pripadajúcu na jednotku času :
![]()
Ďalej predpokladáme, že permeabilita m a permitivita e nezávisia od času, takže ich pri derivácii budeme považovať za konštanty. Na základe vzťahov D = eE a B = mH dostaneme :
![]()
Do posledného integrálu dosadíme vzťahy vyplývajúce z Maxwellových rovníc
![]()
a rozdelíme ho na dva integrály :
![]() (11.3.4.1)
(11.3.4.1)
Druhý z integrálov predstavuje Joulove straty v zvolenom objeme poľa. V zjednodušenom prípade sa o tom možno presvedčiť jeho úpravou, keď si zvolíme objem v tvare valca s prierezom S a dĺžkou d , konštantnú prúdovú hustotu j rovnobežnú s vektorom E a s osou valca. Potom :
![]()
kde Ed = U je elektrické napätie medzi základňami valca, jS = I je prúd tečúci medzi základňami a R je príslušný elektrický odpor.
Prvý z dvoch integrálov si vyžaduje náročnejšiu úpravu. Preto si najprv vypočítame výraz div (H x E) . Operácia divergencia predpisuje derivácie, pričom výraz v zátvorke musíme derivovať ako súčin. Preto pri úprave budeme pri nabla operátore používať indexy symbolizujúce veličinu, na ktorú sa vzťahuje. Pri úpravách použijeme pravidlo o vzájomnej zámene skalárneho a vektorového súčinu v zmiešanom súčine :
Ñ × (H ´ E) = ÑH × (H ´ E) + ÑE × (H ´ E) = (ÑH ´ H) × E - (ÑE ´ E) × H =
= E × rot H - H × rot E
Do prvého z integrálov v rovnici (11.3.4.1) dosadíme namiesto (E × rot H - H × rot E) výraz div (H x E), čím dostaneme :
![]()
pričom sme použili Gaussovu - Ostrogradského vetu na zámenu objemového integrálu na plošný integrál cez uzavretú plochu. Táto plocha uzatvára zvolený objem v elektromagnetickom poli. Rovnica (11.3.4.1) tak dostane konečnú podobu :
![]() (11.3.4.2)
(11.3.4.2)
V prvom integráli vystupuje Poyntingov vektor P = E x H , takže tento člen predstavuje únik elektromagnetickej energie cez uzavretú plochu za jednotku času.
Ak by sa Poyntingov vektor rovnal nule, v uzavretej ploche by ubúdalo elektromagnetickej energie len prostredníctvom Joulových strát. Ak by existovali Joulove straty, ale celková energia v objeme ohraničenom uzavretou plochou by sa nemenila, potom by platila rovnosť :
![]()
To znamená, že Joulove straty by mali byť kompenzované prítokom energie zvonku. Vektor dS má podľa zaužívaných dohôd smer z uzavretej plochy von, a aby aj pravá strana bola kladná, vektor P = E x H musí mať opačný smer ako vektor dS , aby ich skalárny súčin P × dS bol záporný. Potom bude elektromagnetická energia pritekať zvonka do uzavretej plochy.
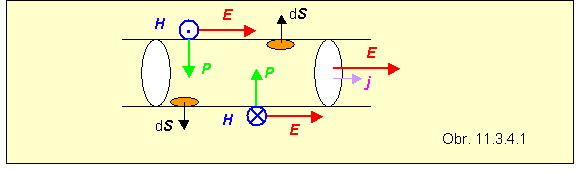
Príklad 11.3.4.1 Dlhým priamym vodičom s kruhovým prierezom tečie elektrický prúd I . Overte si, že v takomto prípade Poyntingov vektor smeruje dovnútra vodiča - zo všetkých strán jeho valcového plášťa .
Riešenie Elektrický prúd je vyvolaný elektrickým poľom s intenzitou E , pričom vodičom tečie prúd s prúdovou hustotou j . Elektrické pole existuje aj mimo vodiča. Tečúci prúd vytvára v okolí vodiča magnetické pole, ktorého smer určíme z Biotovho - Savartovho zákona. Nad vodičom (na obrázku) vektor intenzity magnetického poľa H smeruje pred obrázok, pod vodičom za obrázok. Vektorový súčin P = E x H smeruje v oboch prípadoch dovnútra vodiča.
Kontrolné otázky
- Akými mechanizmami dochádza k stratám energie elektromagnetického poľa ?
- Akým objemovým integrálom možno vo vodiči vyjadriť Joulove straty ?
- Aký smer má Poyntingov vektor na povrchu vodiča, ktorým tečie elektrický prúd ?
- Rozpíšte výraz div (H x E) !
- Na základe vzorca pre Poyntingov vektor ukážte, aký má fyzikálny rozmer !

