Podľa Sommerfeldovej teórie prúdová slučka (elektrón pohybujúci sa po orbite) môže nadobúdať len takú orientáciu vo vonkajšom magnetickom poli, že priemet orbitálneho momentu hybnosti L_z do smeru vonkajšieho magnetického poľa B je celočíselným násobkom, t.j. h/2p .

Tento efekt sa nazýva priestorové kvantovanie orbitálneho momentu. K dodržaniu tejto skutočnosti Sommerfeld zaviedol magnetické kvantové číslo m_l , ktoré udáva smer vektora L tým, že určuje jeho zložku v smere poľa, kde

(13.2.2.13)

kde m_l = 0, ± 1, ± 2, ........, ± l, l –vedľajšie kvantové číslo . (13.2.2.14)

Keďže počet možných hodnôt m_l pre danú hodnotu l je 2l + 1, tak i počet možných orientácií vektora momentu hybnosti L v magnetickom poli je

2l + 1 (obr. 13.2.2.5 ).

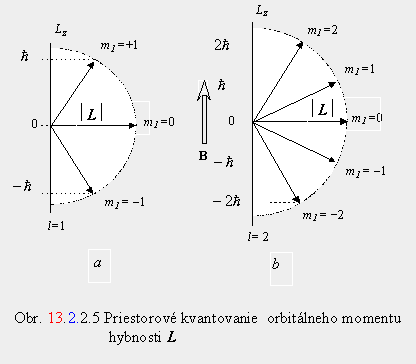
Magnetický moment spojený s pohybom elektrónu po orbite závisí od orbitálneho momentu hybnosti L vzťahom

, (13.2.2.15)

respektíve, keď nahradíme orbitálny moment hybnosti jeho kvantifikátoromlh/2p dostaneme pre veľkosť magnetického momentu elektrónu m v atóme vodíka

(13.2.2.16)

Veličinu eh/4mp nazývame Bohrov magneton m_B . V prítomnosti magnetického poľa o indukcii B hladina energie s daným orbitálnym kvantovým číslom l sa štiepi v magnetickom poli na 2l + 1 podhladín. Energie susedných podhladín sa líšia o energiu

E_m = m_l m_B B. (13.2.2.17)

Separácia energie, ináč identických energetických hladín, poskytuje vysvetlenie Zeemanovho javu.

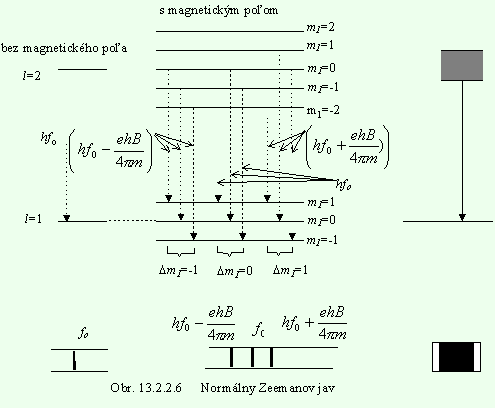
Pretože však zmeny kvantového čísla m_l sú ohraničené na Dm_l = 0, ± 1 rozštiepi sa spektrálna čiara vznikajúca pri prechode medzi dvoma stavmi s rôznymi l len na tri zložky, ako ukazuje obr. 13.2.2.6.

Poznámka: Požiadavku na zmenu kvantového magnetického čísla Dm_l = 0, ±1 určuje tzv. výberové pravidlo, o ktorom ešte pojednáme.

Príklad 13.2.2.5 Elektrón v atóme vodíka sa nachádza v stave f. Určite orbitálny moment hybnosti elektrónu L, maximálnu hodnotu priemetu momentu hybnosti do smeru vonkajšieho magnetického poľa, ako aj magnetický moment vytvorený orbitálnym pohybom elektrónu.

Riešenie  Pre kvantovanie momentu hybnosti platí . Stavu f odpovedá ℓ = 3 a dostávame L = 3,64·10^–34 J·s. Priemet momentu hybnosti L_z = m_l. Jeho maximálna hodnota bude mať magnetické kvantové číslo m_l = 3. Po dosadení dostávame L_z = 3,15·10^–34 J·s. Magnetický moment

_. 

Kontrolné otázky

1. Aký význam má magnetické kvantové číslo m _l ?
2. Čo rozumiete pod priestorovým kvantovaním orbitálneho momentu hybnosti elektrónu?
3. Akým kvantovým číslom je určená zložka orbitálneho momentu v smere vonkajšieho magnetického poľa?
4. Koľko možných orientácií nadobúda priemet L_z?
5. Nakreslite možné priemety L_z pre stav s vedľajším kvantovým číslom l=3.
6. Napíšte súvislosť medzi zložkou orbitálneho momentu hybnosti L_z a magnetickým kvantovým číslom.