 Spinové kvantové číslo ms - priestorové kvantovanie spinového momentu hybnosti
Spinové kvantové číslo ms - priestorové kvantovanie spinového momentu hybnosti
Na základe experimentálnych meraní bolo zistené, že mnohé spektrálne čiary sa v skutočnosti skladajú z dvoch tesne vedľa seba ležiacich oddelených čiar. Príkladom tejto jemnej štruktúry je prvá čiara Balmerovej série vodíka, ktorá vzniká pri prechode medzi hladinami n = 3 a n = 2 vodíkových atómov. Hodnota teoreticky vypočítanej vlnovej dĺžky odpovedajúcej čiary je 656,3 nm, kým v skutočnosti tu existujú dve čiary vzdialené od seba 0,14 nm - efekt síce malý, avšak naznačujúci nesúhlas s teóriou.
V snahe vysvetliť jemnú štruktúru spektrálnych čiar i anomálny Zeemanov jav navrhli S. A. Goudsmit a G. E. Uhlenbeck v roku 1925 hypotézu, podľa ktorej elektrón ma vlastný, vnútorný moment hybnosti nazvaný spinový moment hybnosti S, nezávislý od jeho orbitálneho momentu hybnosti L a určitý magnetický spinový moment ms spojený s týmto vnútorným momentom hybnosti. Goudsmit a Uhlenbeck mali na mysli klasický obraz elektrónu ako nabitej guličky rotujúcej okolo svojej osi. S rotáciou je spojený moment hybnosti a pretože je elektrón záporne nabitý, má magnetický moment ms
![]() . (13.2.2.18)
. (13.2.2.18)
Predstava o elektróne ako o rotujúcej nabitej guličke nebola v súlade s kvantovou mechanikou, avšak v roku 1928 sa Diracovi na základe relativistickej teórie podarilo ukázať, že častica s nábojom a hmotnosťou elektrónu má mať práve takýto vlastný moment hybnosti a magnetický moment, ktorý mu pripísali Goudsmit a Uhlenbeck.
K popisu spinového momentu hybnosti S sa používa spinové kvantové číslo s. Zo spektrálnych údajov ako i neskôr z Diracovej teórie vyplýva, že s môže nadobúdať jedinú hodnotu s = 1/2.
Veľkosť spinového momentu hybnosti S daného elektrónu súvisí so spinovým kvantovým číslom vzťahom
![]() , (13.2.2.19)
, (13.2.2.19)
ktorý je formálne zhodný so vzťahom (13.2.2.11), určujúcim veľkosť orbitálneho momentu hybnosti L pomocou vedľajšieho kvantového čísla l. Priestorové kvantovanie elektrónového spinu sa popisuje spinovým magnetickým kvantovým číslom ms . Rovnako ako vektor orbitálneho momentu hybnosti L môže nadobúdať v magnetickom poli 2l + 1 orientácií od - l, .... 0, ... , + l, môže i vektor spinového momentu hybnosti S nadobúdať 2s + 1 orientácií od -s do +s, t.j. 2 orientácie ( obr. 13.2.2.7), určené hodnotami ms = ± ½. Zložka Sz spinového momentu hybnosti elektrónu pozdĺž magnetického poľa v smere osi z je určená spinovým magnetickým kvantovým číslom ms, ktorý je formálne zhodný so vzťahom (13.2.2.11), určujúcim veľkosť orbitálneho momentu hybnosti L pomocou vedľajšieho kvantového čísla l.
![]() (13.2.2.20)
(13.2.2.20)
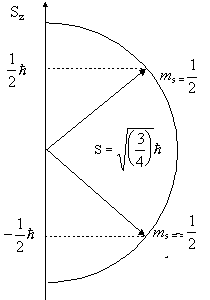
Obr. 13.2.2.7 Priestorové kvantovanie vektora spinového momentu hybnosti S

Priemet spinového magnetického momentu ms do ľubovolnej osi, napr. os z, taktiež nemôže nadobúdať ľubovolné hodnoty. Štúdiom magnetického momentu atómov sa zaoberali Otto Stern a Walter Gerlach v roku 1921, ktorí prvýkrát experimentálne demonštrovali v tom čase ešte neznámy spinový moment elektrónu S a jeho priestorové kvantovanie.
Sternove - Gerlachove pokusy - hoci neumožnili celkom presne merať magnetický moment atómu, získané výsledky postačili pre zásadné a spoľahlivé závery o existencii spinu a spinového magnetického momentu elektrónu.

Kontrolné otázky
- Aký význam má magnetické spinové kvantové číslo ms ?
- Má elektrón v atóme okrem orbitálneho momentu hybnosti L ešte ďalší moment hybnosti? Ak áno, ako sa nazýva?
- Čo charakterizuje veličina „spin“?
- Aký je rozdiel medzi spinom a spinovým magnetickým kvantovým číslom?
- Čo viedlo Uhlenbecka a Gouldsmitha k zavedeniu spinu elektrónu?
- Čo rozumiete pod priestorovým kvantovaním spinového momentu elektrónu S ?
- Koľko možných hodnôt nadobúda spinové magnetické kvantové číslo ms?
- Koľko možných orientácií nadobúda spinový moment hybnosti S?
- Nakreslite pre Vami zvolený prípad priestorové kvantovanie spinového momentu hybnosti.
