Pri skúmaní vlnenia sme sa najčastejšie stretali s harmonickým monochromatickým vlnením s vlnovou dĺžkou l, ktoré možno vyjadriť pri šírení sa v kladnom smere osi x v tvare

(13.3.3.6)

kde u_max je amplitúda vlnenia, w je uhlová frekvencia a k je vlnové číslo, určené vzťahmi w = 2pf , k = 2p/ l .

Harmonickú vlnu, predstavujúcu rovinnú vlnu šíriacu sa v kladnom smere osi x , však možno popísať tiež i kosínusovou vlnou. Túto skutočnosť možno matematicky vyjadriť použitím exponenciálneho zápisu pre rovinnú vlnu

Y(r, t) = A exp[-i(w t-k.r]. (13.3.3.7)

Poznámka: Transformáciu z jednorozmerného na trojrozmerný prípad možno urobiť tým ,že vlnové číslo k nahradíme vektorom k (vektor kolmý na vlnoplochu, a namiesto x bude vystupovať polohový vektor r .

Je známe, že de Broglieho vlny sa nedajú vyjadriť jednoduchým vzorcom, ako je (13.3.3.7), ktorý popisuje nekonečnú radu vĺn s rovnakou amplitúdou A , nakoľko graf závislosti hustoty pravdepodobnosti ÷ Y÷² od x v prípade jednorozmerného pohybu voľnej častice je priamka rovnobežná s osou x. To ale znamená, že častica má všade rovnakú pravdepodobnosť, že bude detekovaná a teda môže byť kdekoľvek pozdĺž osi x. Takáto vlnová funkcia je nenormovateľná. Preto vlnovej reprezentácii pohybujúcej sa voľnej častici nebude odpovedať monochromatická vlna, ale bude jej odpovedať vlnové klbko, ktoré je znázornené na obr. (13.3.3.1), kde hustota pravdepodobnosti výskytu je vyjadrená v tvare súčinu dvoch funkcií, z ktorých prvá j( x, y, z) je len funkciou súradníc a druhá len funkciou času

Y(r, t) = j (x, y, z) e^-iwt = j (x, y, z) exp [-i(w t]. (13.3.3.8)

Obr. 13.3.3.1 Tvar reálnej (a) a imaginárnej (b) zložky jednotlivých rovinných vĺn a výsledný tvar reálnej a imaginárnej zložky vlnového klbka.

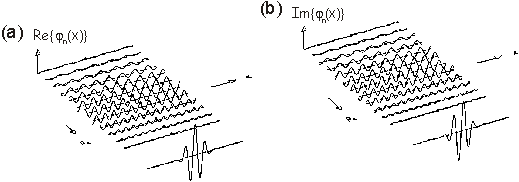
Poznámka: Ako príklad vlnového klbka možno uviesť prípad, kedy sa skladajú dve zvukové vlny s rovnakou amplitúdou, ale s rôznymi kmitočtami f₁ a f₂. Výsledným vlnením je vlnenie, ktorého amplitúda sa periodicky mení (striedavo sa zoslabuje a zosilňuje) a frekvencia vlnenia sa rovná priemernej hodnote frekvencií, t.j. f = (f ₁+ f ₂)/2

Vlnové klbko je možné popísať superpozíciou radu vlnení, ktoré sa líšia o dw v uhlovej frekvencii a o dk vo vlnovom čísle. Rýchlosť, s ktorou sa šíri maximum vlnového balíka nazývame grupovou rýchlosťou w. Grupová rýchlosť je určená vzťahom

(13.3.3.9)

Odôvodnenie a bližšie objasnenie grupovej rýchlosti čitateľ nájde v prvej časti v kapitole je 6.2.7 a rovnicou 6.2.7.6.

Príklad 13.3.3.3 Ukážte, že De Broglieho vlnové klbko spojené s pohybujúcou sa časticou sa pohybuje rovnakou rýchlosťou ako častica.

Riešenie  Vyjadrime si vzťah pre uhlovú frekvenciu a pre vlnové číslo de Broglieho vlny prislúchajúcej častici s pokojovou hmotnosťou m0, ktorá sa pohybuje s rýchlosťou v :

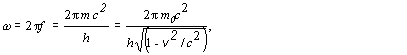  (1)

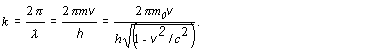  (2)

Grupovú rýchlosť, určenú vzťahom (13.3.3.9) resp. (6.2.7.6) , vyjadrime ako

(3)

Po dosadení derivácií

do rovnici (3), dostávame rovnosť w = v , ktorá hovorí: De Broglieho vlnové klbko spojené s pohybujúcou sa časticou sa pohybuje s tou istou rýchlosťou ako častica.

Kontrolné otázky

1. Nakreslite a vysvetlite pojem vlnové klbko.
2. Čím sa líši monochromatická harmonická vlna od vlnového klbka?
3. Má vlnové klbko konštantnú amplitúdu?
4. Nakreslite graf závislosti hustoty pravdepodobnosti pre voľnú časticu a zdôvodnite ho.
5. Akú frekvenciou má vlnové klbko, ktoré vzniká superpozíciou dvoch vlnení s blízkymi frekvenciami a rovnakými amplitúdami?
6. S akou rýchlosťou sa šíri maximum vlnového klbka
7. Pohybuje sa De Broglieho vlnové klbko spojené s pohybujúcou sa časticou s tou istou rýchlosťou ako častica?