Časová Schrödingerova rovnica

Nová mechanika odpovedajúca „vlno-častici", ktorá tak výborne poslúžila pri vysvetlení experimentálnych výsledkov získaných koncom 19. storočia, priniesla zároveň neprekonateľné problémy pri formulovaní pohybovej rovnice. Pohybové rovnice v klasickej fyzike (Newtonova pohybová rovnica pre mechaniku, Maxwellove rovnice pre teóriu elektromagnetického poľa a vlnová rovnica pre vlnenie ) nám na základe začiatočných a okrajových podmienok určujú stav v ľubovolnom časovom okamihu. Hovoríme o deterministickom vývoji v čase. V kvantovej fyzike vlno-častíc nemôžeme hovoriť o deterministickom určení, ale len o pravdepodobnostnom určení, pretože štvorec absolútnej hodnoty vlnovej funkcie určuje pravdepodobnosť uvažovaného stavu. Pohybová rovnica popisujúca stav vlno-častice (mikročastice) by nám mala poskytnúť na základe znalosti vlnovej funkcie v určitom okamihu t₀ (súčasnosť) vlnovú funkciu v ľubovoľnom okamihu v budúcnosti. Kvantovo-mechanická pohybová rovnica musela v sebe spájať vlnové a súčasne aj korpuskulárne vlastnosti mikroskopických častíc. Tento problém riešili v rokoch 1925 - 1926 rakúsky fyzik Erwing Schrödinger a nemecký fyzik Werner Heisenberg. Základná pohybová rovnica kvantovej fyziky – Schrödingerova rovnica nesie meno po svojom objaviteľovi a umožňuje predpovedať stavy systémov, ktorých rýchlosti sú značne menšie ako rýchlosť svetla vo vákuu. Existuje viac spôsobov odvodenia Schrödingerovej rovnice. Čitateľovi ponúkame „najbežnejší“ spôsob odvádzania (nie je totožný s pôvodným odvodením rovnice), vychádzajúci z priradenia vlnovej funkcie voľnej vlno-častici.

Klasická fyzika na základe z Newtonovej pohybovej rovnice a zadaných začiatočných podmienok v časovom okamihu t, presne určí pohybový stav skúmaného objektu v ľubovolnom časovom okamihu t. Hovoríme o deterministickom vývoji, ktorý vieme presne dopredu určiť.

Na základe DeBroglieho hypotézy možno voľnej častici s hmotnosťou m, energiou E, polohovým vektorom r priradiť netlmenú monochromatickú harmonickú vlnu s uhlovou frekvenciou w , šíriacu sa v smere vlnového vektora k, popísanú vlnovou funkciu (13.3.3.7)

Y (r, t) = A exp [-i (w t –k.r )] .

Poznámka: Pod voľnou časticou rozumieme časticu, na ktorú nepôsobia žiadne sily, t.j. pohybuje sa priamočiaro s konštantnou rýchlosťou a ktorá má konštantnú potenciálnu energiu.

Pre zjednodušenie v prvom kroku uvažujme vlnu šíriacu sa v kladnom smere osi x, pre ktorú platí

Y (x, t) = A exp [-i (w t –k x)] .

Postupnými úpravami si ukážeme jej viaceré možné vyjadrenia:

Y (x, t) = A exp [-i (w t –2p x / l)] = A exp [-i (E t/ ? –2p p x / h)] = A exp[-i (E t/ ? – p x / ?)],

kde sme použili vzťahy pre veľkosť vlnového vektora k = 2 p / l , De Broglieho vlnovú dĺžku l = h / p a vzájomnú súvislosť energie a uhlovej frekvencie, t.j. rovnicu E = hf = ? w. Ďalšou matematickou úpravou získame vzťah pre vlnovú funkciu, pomocou ktorého odvodíme Schrödingerovu rovnicu., t.j.

Y (x, t) = A exp [-i (w t –2p x / l)] = A exp [-i (E t/ ? –2p p x / h)] = A exp[-i (E t/ ? – p x / ?)],

Y (x, t) = = A exp [-i (E t – p x) / ? ] = A exp [i (p x –E t) / ? ] , (13.4.2.1)

kde p je veľkosť vektora hybnosti voľnej vlno-častici, pohybujúcej sa v smere osi x .Určime prvé a druhé derivácie vlnovej funkcie podľa x-ovej súradnice:

(13.4.2.2)

(13.4.2.3)

V rovnici (13.4.2.2) si osamostatnime súčin p y(x,t), pre ktorý platí

_. (13.4.2.4)

Rovnica (13.4.2.4) ukazuje ako zavedieme k fyzikálnej veličine hybnosť jej operátor, t.j. operátor hybnosti , ktorý bol definovaný vzťahom (13.4.1.6). Obdobne v rovnici (13.4.2.3) osamostatníme súčin p² y(x,t),

. (13.4.2.5)

Rovnica (13.4.2.5) ukazuje ako zavedieme k fyzikálnej veličine štvorcu hybnosti jej operátor, t.j. operátor kvadrátu hybnosti, ktorý označíme definovaný rovnicou (13.4.1.7).

Určime prvú deriváciu vlnovej funkcie podľa času

. (13.4.2.6)

V rovnici (13.4.2.6) osamostatnime súčin

, (13.4.2.7)

ktorý obdobne ukazuje ako zavedieme k fyzikálnej veličine energia častice, jej operátor definovaný rovnicou (13.4.1.8).

Keďže skúmame voľnú časticu, celková energia voľnej častice je určená je kinetickou energiou, ktorú možno zapísať pomocou kvadrátu hybnosti v tvare

(13.4.2.8)

Ak rovnicu (13.4.2.5) predelíme dvojnásobkom hmotnosti častice dostávame rovnicu

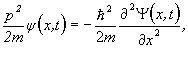(13.4.2.9)

a porovnáme rovnice (13.4.2.8) a (13.4.2.9) dostaneme jednorozmernú rovnicu pre voľnú časticu pohybujúcu sa v kladnom smere osi x

(13.4.2.10)

ktorá sa nazýva jednorozmerná Schrödingerova rovnica pre voľnú časticu. Problém môžeme zovšeobecniť na trojrozmerný prípad, v ktorom vystupujú kvadráty zložiek hybností p_x², p_y² a p_z²

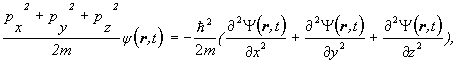
resp. s využitím Laplaceovho operátora D

,

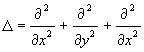a porovnaním dostaneme rovnicu

, (13.4.2.11)

resp.

, (13.4.2.12)

ktorú nazývame trojrozmerná časová Schrödingerova rovnica pre voľnú časticu. Rovnicu (13.4.2.12) splňuje každá vlnová funkcia y(r, t) prislúchajúca rovinnej vlne. Možno predpokladať, že rovnica bude platiť aj pre vlnenie, ktoré je superpozíciou rovinných vĺn, kedy hovoríme o vlnovom balíku.

Ak sa častica nachádza v potenciálovom poli, jej celkovú energiu možno vyjadriť ako súčet kinetickej a potenciálnej energie

.

a jednorozmerná základná rovnica kvantovej fyziky bude mať v tomto prípade tvar

(13.4.2.13)

resp, v trojrozmernom prípade

. (13.4.2.14)

V prípade zápisu pomocou Hamiltonovho operátora H ( Hamiltoniánu), definovaného rovnicou (13.4.1.7), možno časovú Schrödingerovu rovnicu

zapísať v tvare

(13.4.2.15)

Táto rovnica v sebe spája vlnovú a klasickú pohybovú rovnicu a dnes ju nazývame časová Schrödingerova rovnica na počesť Ervina Schrödingera. Rovnica (13.4.2.15) je základnou rovnicou kvantovej mechaniky.

Pre zachovanie historickej objektivity treba poznamenať, že nezávisle od Schrödingera odvodil podobnú rovnicu Werner Heisenberg.

­­­­­­­­­­­­­­­­­­­­­­­­­­

Príklad 13.4.2.1 Ukážte, že ak vlnová funkcia y₁ (x,t) , y₂ (x,t) sú dve riešenia Schrödingerovej rovnice pre potenciálnu energiu E_p (x.t), potom riešením tejto rovnice je aj ich ľubovoľná lineárna kombinácia .

Riešenie  Vlnové funkcie y1 (x,t) a, y2 (x,t) sú dve riešenia Schrödingerovej rovnice, takže platí: 

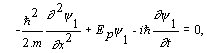(1)  

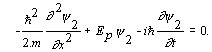(2) 

Dokážeme, že i lineárna kombinácia jednotlivých riešení, t.j. vlnová funkcia y( x, t) 

y( x, t ) = c1. y1 (x, t) + c2 y2 (x, t), 

je riešením Schrödingerovej rovnice a že platí 

Po dosadení za y (x, t) a úprave dostávame

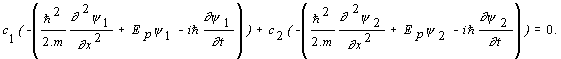
Keďže vlnové funkcie y1, y2 sú riešením Schrödingerovej rovnice, výrazy v zátvorkách sa rovnajú nule a z toho vyplýva, že i lineárna kombinácia daných rovníc je riešením Schrödingerovej rovnice.

 

Príklad 13.4.2.2 Odhadnite, aká je pravdepodobnosť, že elektrón, ktorého stav je opísaný vlnovou funkciou

sa nachádza v guľovej vrstve s polomerom r₀ a hrúbkou dr = 0,01 r₀ .

Riešenie  Vzhľadom na to, že dr « r0 , nie je nutné pravdepodobnosť počítať pomocou integrálu. Stačí uvažovať vzťah p » y y* d t.. Vzhľadom na radiálnu symetriu funkcie objemový element vyjadríme v tvare d t = 4 p r2 dr

 

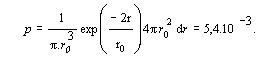
Stacionárna Schrödingerova rovnica

Základnú rovnicu kvantovej fyziky možno v prípade stacionárnych stavov uparviť na tzv. stacionárnu pohybovú rovnicu, ktorá nebude funkciou času. Stacionárne stavy sú charakterizované určitými hodnotami energie a pre takéto stavy možno vlnovú funkciu Y vyjadriť v tvare súčinu dvoch vlnových funkcií, z ktorých jedna (j) vyjadruje závislosť na priestorových súradniciach a druhá (F) časovú závislosť:

Y(r,t) = j(r) F(t) . (13.4.2.16)

Uvažujem opäť len jednorozmerný prípad, kedy vlnová funkcia bude mať tvar

Y(x,t) = j(x) F(t) . (13.4.2.17)

Po dosadení vlnovej funkcie tvaru (13.4.2.17) do časovej jednorozmernej Schrödingerovej rovnice (13.4.2.13) dostaneme

.

Ak poslednú rovnicu vydelíme súčinom j(r) F(t) a odseparujeme premenné, dostaneme separovateľnú diferenciálnu rovnicu

,

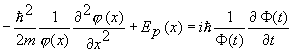ktorú možno zapísať ako rovnosť dvoch funkcií. Nakoľko sú to funkcie rôznych premenných, rovnica bude mať riešenie len ak obidve funkcie sa budú rovnať konštante E , t.j.

F(x) = G(t) =E

Potom možno zapísať F(x) = E v tvare

(13.4.2.18)

Rovnica (13.4.2.18) sa nazýva stacionárna jednorozmerná Schrödingerova rovnica. Pre trojrozmerný prípad má tvar

(13.4.2.19)

Schrödingerovu stacionárnu rovnicu (13.4.2.19) možno zapísať pomocou Hamiltonovho operátora H v tvare

(13.4.2.20)

kde j (r) sú vlastné funkcie a E vlastné hodnoty operátora energie H .

Z podmienky G(t) =E dostaneme

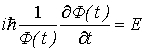
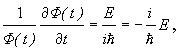
Po integrovaní poslednej rovnice dostaneme

.

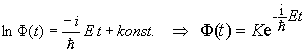kde K je konštanta. Na základe uvedeného možno vlnovú funkciu pre jednorozmerný pohyb vyjadriť v tvare

(13.4.2.21)

a po zovšeobecnení na trojrozmerný prípad v tvare

(13.4.2.22)