 Heisebergové vzťahy neurčitosti
Heisebergové vzťahy neurčitosti
Keď sa Ervínovi Schrödingerovi podarilo odvodiť pohybovú rovnicu, ktorá dokázala spojiť vlnové a korpuskulárne vlastnosti mikročastice, odštartovala sa tým diskusia ako súvisí makrosvet, v ktorom žijeme a pozorujeme ho, s nehmatateľným a do istej miery abstraktným mikrosvetom vlno-častíc. Natískala sa otázka, či je hranica medzi mikrosvetom a makrosvetom a či je vôbec možné nahliadnuť za hranice kvantového mikrosveta.
V roku 1926 sa pokúsil Werner Heisenberg (vtedy len 25 ročný nemecký fyzik) na základe poznatkov z kvantovej teórie interpretovať pozorovanie mikrosveta. Na základe jeho výsledkov v roku 1927 Werner Heisenberg postuloval nerovnosti, ktoré sa dnes nazývajú Heisenbergove vzťahy neurčitosti. Podľa prvého vzťahu nie je možné súčasne presne zmerať polohu r i hybnosť častice p. Súčin nepresnosti týchto veličín nikdy nemôže byť menší ako hodnota h /4p .
Prvý Heisenbergov princíp neurčitosti určuje ohraničenie
Dx Dpx ³ h/4p,
Dy Dpy ³ h/4p, (13.4.3.1)
Dz Dpz ³ h/4p,
kde Dx je neurčitosť v určení polohy častice a Dpx je neurčitosť v určení zložky jej hybnosti do príslušného smeru x.
Druhý Heisenbergov vzťah neurčitosti určuje ohraničenie
DE Dt ³ h/4p (13.4.3.2)
a tvrdí, že ani súčin neurčitosti v určení energie DE a časového intervalu Dt, v ktorom sa meranie uskutočnilo, nemôže nadobudnúť ľubovoľne malú hodnotu. Tento súčin nikdy nemôže byť menší ako h/4p. Zo vzťahu vyplýva, že žiaden vlnový proces ohraničený v čase Dt nemôže byť monochromatický. Čím kratší je čas existencie určitého energetického stavu, resp. čas vymedzený na jeho pozorovanie, tým s menšou presnosťou môžeme určiť energiu tohto stavu. Tento vzťah má závažný dôsledok pre platnosť zákona zachovania energie: energia sa zachováva s presnosťou nanajvýš rovnou DE= h/4pDt.

Riešenie Vychádzame z Heinsenbergovho vzťahu neurčitosti (13.4.3.1), kde neurčitosť hybnosti Dp je Dp = m. D v. Neurčitosť súradníc D x môžeme určiť s presnosťou rozmeru atómu, t.j. 10-10m. Potom

Je zrejmé, že pri tak veľkej neurčitosti rýchlosti si nemôžeme dráhu elektrónu v atóme predstavovať ako spojitú trajektóriu v klasickom zmysle.
Príklad 13.4.3.2 Atóm vyžiari v priebehu časového intervalu Dt = 10-8 s fotón vlnovej dĺžky l = 600 nm. Určite neurčitosti v stanovení jeho energie, frekvencie a vlnovej dĺžky.
Riešenie Neurčitosť energie nájdeme z Heinsenbergovho vzťahu, určeného rovnicou (13.4.3.2) DE Dt ³ h/4p
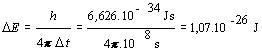 .
.
Neurčitosť frekvencie Df bude
![]() .
.
Neurčitosť vlnovej dĺžky nájdeme derivovaním vzťahu l = c f ako
![]()
Príklad 13.4.3.3 Pomocou Heisenbergovho princípu neurčitosti dokážte, že elektróny sa nemôžu nachádzať v atómovom jadre.
Riešenie Úlohu môžeme riešiť dvoma spôsobmi.
Prvý spôsob riešenie: Pre elektrón viazaný v jadre je neurčitosť jeho polohy Dx rádovo rovná 10-14 m, čo je rozmer jadra. Pre neurčitosť rýchlosti Dv vyplýva
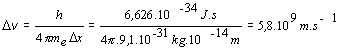 .
.
Všimnime si, že nám vyšla hodnota väčšia ako rýchlosť svetla, čo je nereálne a teda elektrón sa nemôže nachádzať v jadre.
Druhý spôsob riešenia: Znovu vyjdeme zo vzťahu neurčitosti Dx Dpx ³ h/4p, z ktorého však teraz stanovíme neurčitosť energie DE a určíme, či vypočítaná hodnota je reálna. Zodpovedajúca neurčitosť hybnosti Dpx (a teda aj minimálna hybnosť) po dosadení hodnôt bude D p ³ 1,1.10-20 kg.m.s-1. Z relativistického vzťahu pre celkovú energiu
![]()
sa ľahko presvedčíme, že kinetická energia Ek častice s takouto hybnosťou je značne väčšia ako jeho pokojová energia E0 = m0c2. Pre výpočet kinetickej energie stačí použiť zjednodušený relativistický vzťah
![]()
Táto hodnota je nereálne vysoká, pretože aj najrýchlejšie elektróny vznikajúce pri b - rozpade jadier majú len zlomok takejto energie. Vypočítaná hodnota značne prevyšuje väzbovú energiu na nukleón a niet dôvodu, že by pre elektrón mala byť značne vyššia. Preto elektrón nemá šancu sa v jadre udržať.
Príklad 13.4.3.4 Odhadnite šírku čiary Dl a rozptyl frekvencie Dn pre svetelný impulz rubínového lasera, ktorého doba trvania je t = 1 ns a vlnová dĺžka l = 630 nm.
Riešenie: Na odhad použijeme Heisenbergov princíp neurčitosti v tvare DE Dt ³ h/2p. Neurčitosť v čase Dt odhadneme, že je rádovo rovná dobe trvania impulzu lasera (Dt ≈ t). Neurčitosť energie E = h c /l vyjadríme pomocou Dl, resp. Df
![]() ,
,
resp.
![]()
Potom
![]()
![]()
Poznámka: O tom, ktoré veličiny v kvantovej fyzike nadobúdajú presné (ostré) hodnoty, t.j. sú súčasne presne merateľné hodnoty, rozhoduje komutátor operátorov týchto veličín. S definíciou komutátora, ako i jednotlivých operátorov sa čitateľ môže oboznámiť v časti 13.4.2 alebo v monografiách kvantovej fyziky.
Kontrolné otázky
- Sú všetky veličiny v kvantovej mechanike súčasne presne merateľné?
- Môžeme na základe lepšej rozlišovacej presnosti moderných prístrojov určovať súčin neurčitosti polohy častice s neurčitosťou zložky hybnosti s menšou presnosťou ako je ħ/10.
- Vymenujte aspoň dve dvojice fyzikálnych veličín, ktoré nie sú súčasne presne merateľné.
- Vyslovte Heisenbergove vzťahy a vysvetlite ich význam.
- Môžeme šírku spektrálnej čiary určovať s ľubovolnou presnosťou ?
- Uveďte aká je najmenšia nepresnosť, s ktorou môžeme určovať súčin neurčitosti polohy a neurčitosti zložky hybnosti.
- Prečo nemôžeme hovoriť o determinizme fyziky z hľadiska Heisenbergových vzťahov neurčitosti?
- Na základe Heisenbergových vzťahov neurčitostí sa nedá hovoriť pri pohybe elektrónu okolo jadra o jeho trajektórií. Prečo?
- Ako možno vysvetliť prirodzenú šírku spektrálnej čiary?
- Ako sa zmení energia fotónu, keď sa zmenší vlnová dĺžka svetla l na polovicu?
