V predchádzajúcich častiach tohoto paragrafu sme sa snažili Vám priblížiť základné pojmy a vybrané problémy kvantovej mechaniky (tie najľahšie). Kompaktnosť učiva by požadovala ukázať riešenie i pre nasledovné sústavy:

· častica viazaná v nekonečnej hlbokej potenciálovej jame v dvojrozmernom a trojrozmernom prípade ;

· častica viazaná v konečne hlbokej jednorozmernej potenciálovej jame;

· harmonický oscilátor;

· atóm vodíka na báze riešenia Schrödingerovej rovnice;

Taktiež by mohlo byť zaujímavé vysvetliť javy, ktoré sú dôsledkami platnosti kvantovej fyziky, s ktorými sa v technickej praxi stretávame veľmi často ako napríklad:

· tunelový jav;

· lasery,…

Z dôvodov časovej náročnosti a zvýšených nárokov na matematický aparát tieto časti v tomto kurze neuvádzame. Dychtivý študent ich však nájde v každej základnej učebnici kvantovej mechaniky. Poznatky týkajúce sa horeuvedených skutočností môžno zhrnúť nasledovne:

· Energie elektrónu zachyteného v dvojrozmernej nekonečnej potenciálovovej jame, sú kvantované a získame ich nahradením lineárneho rozmeru L dvomi rozmermi L _x a L _y. a nahradením hlavného kvantového číslo n zložkami n_x a n_y , ktoré dosadíme do rovnice (13.5.2.10) resp. (13.5.2.5)

,

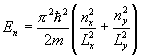kde n_x je kvantové číslo , pre ktoré je prispôsobená vlnová funkcia šírke L_x resp. kde n_y je kvantové číslo , pre ktoré je prispôsobená vlnová funkcia šírke L_y.

Poznámka: Obdobne sa postupuje pre trojrozmerný prípad, prezentujúci pravouhlú krabicu.

· Energie odpovedajúce kvantovým stavom atómu vodíka získame riešením trojrozmernej Schrödingerovej rovnice, kde potenciálna energia je určená

,

a dovolené kvantové stavy atómu vodíka odpovedajú dovoleným kvantovaným energiám

kde hlavné kvantové číslo n = 1,2,3,…

Energie E_n sú zhodné so vzťahom určeným z Bohrovho modelu atómu vodíka. Normovaná vlnová funkcia základného stavu atómu vodíka , získaná riešením trojrozmernej Schrödingerovej rovnice transformovanej do sférických súradníc, má tvar

,

kde a je konštanta s rozmerom dĺžky, tzv. Bohrov polomer atómu.

· Energie odpovedajúce kvantovým stavom jednorozmerného kvantového harmonického oscilátora, t.j. častici pohybujúcej sa pod účinkom sily úmernej výchylke, ale opačného smeru (F = -Kx, K je konštanta) sú kvantované a určené vzťahom

kvantové číslo n = 0,1,2,… .

Pre základný stav, energia harmonického oscilátora je rovná najnižšej hodnote

E₀= h f / 2 = hw/4p.

· Častica s energiou E dopadajúca na bariéru ( napr. alfa častica dopadajúca na atóm) sa podľa klasickej fyzike vždy odrazí od bariéry s potenciálnou energiou E_po > E. V kvantovej fyzike bolo pozorované a vypočítané, že hustota pravdepodobnosti príslúchajúca takejto častici má konečnú hodnotu. Častica môže takúto bariéru pretunelovať. Pravdepodobnosť, že daná častica o hmotnosti m a energii E pretuneluje bariérou s výškou E_p s hrúbkou d, je určená koeficintom prechodu T

T @ e^—2kd,

kde

.

Príklad 13.5.3.1 : Dokážte, že vlnová funkcia je riešením Schrödingerovej rovnice pre jednorozmerný harmonický oscilátor.

Riešenie  Schrödingerova rovnica pre jednorozmerný harmonický oscilátor má tvar:

.

Po dosadení danej funkcie, derivovaní a úprave dostávame:

.

Zadaná funkcia bude riešením, ak súčet členov, v ktorých vystupuje x² sa rovná nule,

t.j..

Z tejto podmienky dostávame pre konštantu

.

Pre energiu E potom platí.

.

Energia je najnižšou možnou energiou harmonického oscilátora. Voláme ju tiež energia nulových kmitov.