 Rovnica spojitosti elektrického prúdu
Rovnica spojitosti elektrického prúdu
Predstavme si, že v nejakom prostredí (napr. vo vodiči) tečie elektrický prúd, obr. 9.4.1. Na obrázku čiary, po ktorých sa pohybujú náboje nazývame prúdnice. Vektory prúdovej hustoty j ležia na dotyčniciach k prúdniciam.
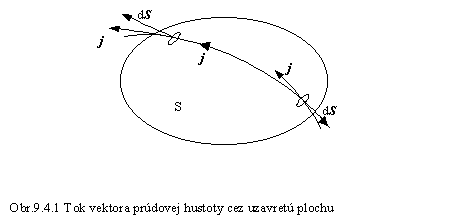
Vložme do prostredia myslenú uzavretú plochu S, ktorá je hranicou objemu V vnútri tejto plochy. Množstvo náboja, ktoré preteká cez plôšku dS je
![]()
Vypočítajme teraz náboj, ktorý vytečie cez plochu S von za čas dt
![]() (9.4.1)
(9.4.1)
Znamienko mínus vyjadruje, že v objeme V náboja ubúda, Q je celkový náboj v tomto objeme. Náboj, ktorý ubudol v objeme V, sa objaví za jeho hranicami, pretože to vyplýva zo zákona zachovania náboja. Rovnica (9.4.1) je matematickým vyjadrením zákona zachovania náboja. Túto rovnicu tiež nazývame rovnicou spojitosti (kontinuity) elektrického prúdu v integrálnom tvare. Ak sa náboj vnútri plochy S s časom nemení (t.j. koľko náboja do plochy vteká, toľko ho z nej aj vyteká), potom pre takýto stacionárny prípad máme
![]() (9.4.2)
(9.4.2)
Prepíšeme teraz rovnicu (9.4.1) do diferenciálneho tvaru. Náboj vnútri plochy je rozložený s objemovou hustotou r. Náboj Q vnútri plochy môžeme napísať ako
![]()
a rovnica (9.4.1) použijúc vetu Gaussa – Ostrogradského z matematiky bude
![]()
Z tejto rovnice priamo vyplýva
![]() (9.4.3)
(9.4.3)
Rovnica (9.4.3) je rovnica spojitosti elektrického prúdu v diferenciálnom tvare. Zaviedli sme parciálnu deriváciu, lebo objemová hustota náboja je vo všeobecnosti funkciou nielen času, ale aj polohy objemového elementu dV.
Rovnica (9.4.1), prípadne (9.4.3), patrí medzi základné rovnice v elektrodynamike.
Príklad 9.4.1: Jedným z dôsledkov rovnice spojitosti je jav Maxwellovej relaxácie nerovnovážneho náboja, ktorý spočíva v nasledujúcom: vytvorme situáciu, napr. injektovaním balíka elektrónov do vodiča, ktorá privedie k prebytku elektrónov v nejakom objeme. Po zániku injektáže sa budú elektróny vplyvom vzájomného odpudzovania z tohoto objemu rozptyľovať. Vypočítajte ako sa bude s časom meniť objemová hustota náboja v nejakom zvolenom objeme.
Riešenie Použijeme rovnice
![]() ,
, ![]() ,
, ![]() .
.
Úpravami a kombinovaním rovníc
![]() , odkiaľ
, odkiaľ
![]() .
.
Riešením tejto rovnice je časová závislosť objemovej hustoty náboja
![]() .
.
Poznámka: tM = e0 / s je tzv. Maxwellov relaxačný čas, ktorý je charakteristikou návratu vodiča do rovnovážneho stavu. Za časový interval tM klesne hustota náboja v sledovanom objeme z počiatočnej hodnoty r0 e-krát. Pre kovy je tento čas 10-15 - 10-13 s, pre polovodiče 10-13 - 10-10 s, pre izolanty s iónovou vodivosťou aj celé hodiny. Nadbytočný náboj sa v dôsledku odpudivých síl nakoniec objaví na povrchu telesa.
Kontrolná otázka
- Čo môžete povedať o tvare prúdnic vychádzajúc z (9.4.2)?
