Budeme sa zaoberať pohybom nabitých častíc vo vákuu. Najjednoduchšie je získať voľné elektróny pomocou termoelektrickej emisie, čo je jav, v ktorom sa z horúceho povrchu kovu uvoľňujú elektróny. Tieto elektróny vstupujú do elektrického poľa, v ktorom sa urýchlia.

Na obr. 9.7.1 je náčrt zariadenia, skladajúceho sa z urýchľovacej časti a z vychyľovacej časti.

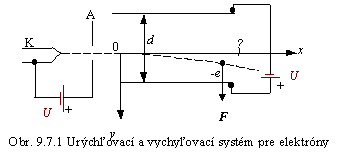
Elektrón opustí katódu K s malou rýchlosťou, ktorú budeme považovať za približne rovnú nule. V elektrickom poli medzi katódou a anódou A sa elektrón urýchli. Rýchlosť vypočítame pomocou zákona zachovania mechanickej energie. Pri katóde je kinetická energia elektrónu rovná nule a potenciálna je eU_A (U_A je potenciál na anóde, U_K = 0). V silovom elektrickom poli sa kinetická energia elektrónu zvýši na úkor jeho potenciálnej energie. Na úrovni anódy bude potenciálna energia elektrónu rovná nule a jeho kinetická energia bude mv²/2. Z rovnice zákona zachovania mechanickej energie

vyjadríme rýchlosť elektrónu

.

Elektrón preletí rovnomerne priamočiaro vzdialenosť medzi anódou a vychyľovacím kondenzátorom, na ktorom je napätie U_v. Elektrické pole v kondenzátore je homogénne, a preto pohyb elektrónu bude formálne rovnaký ako pohyb hmotného bodu v tiažovom poli pri vodorovnom vrhu. V našom prípade bude na elektrón pôsobiť vychyľovacia sila F = ma = eE_v = eU_v/d, kde d je vzdialenosť medzi platňami kondenzátora. Zrýchlenie elektrónu spôsobené vychyľovacou silou je

.

Použijeme rovnice pre súradnice elektrónu (jeho pohyb je „vodorovným“ vrhom v homogénnom elektrostatickom silovom poli) z vodorovného vrhu (zameníme zrýchlenie g zrýchlením a, počiatočné podmienky sú x₀ = 0, y₀ = 0, v_0x = v, v_0y = 0)

Vypočítame polohu elektrónu na konci kondenzátora, ktorý má dĺžku l. Súradnica x = l a z rovnice pre x vypočítame čas potrebný na prelet kondenzátora a dosadíme ho do rovnice pre y. Dostaneme

t.j. vychýlenie nezávisí ani od hmotnosti ani od náboja. Ak by sme celý pokus zopakovali s oveľa ťažším iónom, jeho poloha na konci vychyľovacieho kondenzátora by bola taká istá. Dá sa to vysvetliť tak, že ťažký ión sa urýchli na menšiu rýchlosť a vychyľovacia sila bude môcť pôsobiť dlhší čas.

Vychýlené elektróny musia dopadať na zbernú elektródu, ktorá je pripojená ku kladnej svorke zdroja. Tak sa uzatvorí prúdový okruh. Letiace vo vákuu elektróny tiež vytvárajú elektrický prúd, ktorý pokračuje vo vodičoch a v zdroji.

Poznámka 1: Pozri pohyb elektrónu v radiálnom elektrickom poli.

Poznámka 2: Pohyb elektrónu v homogénnom elektrostatickom poli bol využitý i pri meraní náboja elektrónu.

Príklad 9.7.1: Elektrón je vystrelený proti záporne nabitej vodivej rovine. Rovina, v ktorej leží jeho trajektória je kolmá na nabitú rovinu. Ako sa bude elektrón pohybovať, ak predpokladáme, že sa nedotkne nabitej roviny?

Riešenie  Elektrické pole v okolí rozľahlej nabitej roviny je homogénne a jeho intenzita je E = s/2e₀ , kde s je veľkosť povrchovej hustoty náboja. V takomto poli na elektrón pôsobí konštantná sila F = eE , ktorá elektrón odpudzuje od nabitej roviny a je na túto rovinu kolmá. Zvolíme si súradnicovú sústavu s osou x na nabitej rovine a s osou y smerujúcou od tejto roviny. Osi x, y ležia v rovine trajektórie elektrónu. Pohybové rovnice elektrónu sú

a .

Z týchto rovníc vypočítame zložky rýchlosti a z nich súradnice x, y ako funkcie času. Riešenia musia vyhovovať počiatočným podmienkam: x₀ = 0 , y₀ = h (elektrón bol vstrelený z výšky h nad nabitou rovinou z bodu, ktorý ležal na osi y), v_0x = v₀ cos a , v_0y = v₀ sin a , kde uhol a je medzi vektorom rýchlosti v₀ a osou x.

Riešenia sú

, .

Trajektória elektrónu je parabola.

Kontrolné otázky

1. V príklad 9.7.1 sme neuvažovali tiaž elektrónu. Odhadnite, či sme sa tým dopustili veľkej chyby.
2. V texte tohto paragrafu je veta „Elektrón preletí rovnomerne priamočiaro vzdialenosť medzi anódou a vychyľovacím kondenzátorom“. Čím si vysvetlíte takýto pohyb elektrónu? Je ešte na obr. 9.7.1 úsek, ktorý by elektrón preletel takýmto spôsobom?
3. Mohol by sa rovinný kondenzátor v príklade 9.7.1 použiť na separáciu elektrónov podľa energií?