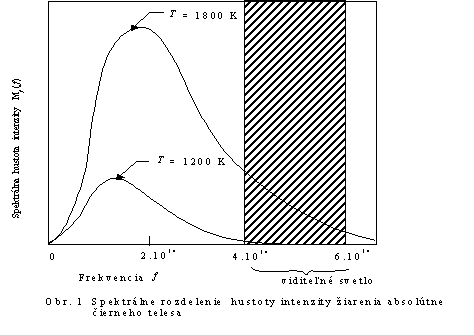
Planckov zákon vyžarovania
Planckov zákon vyžarovania
Problematikou vyžarovania absolútne čierneho telesa sa zaoberal Max Planck. Pri odstraňovaní nesúladu teoreticky odvodenej krivky vyžarovania, určenej Rayleighovým a Jeansovým zákonom Max Planc vychádzal:
· z predpokladu, že ekvipartičná teoréma platí len pre spojité rozdelenie možných energií;
· pripustil hypotézu, že energia elektromagnetickej vlny s frekvenciou f sa nevyžaruje z povrchu telesa spojite , ale je v skutočnosti kvantovaná v jednotkách hf , kde Planckova konštanta h = 6,624 . 10-34 J.s .
Na základe týchto predstáv kvantovej fyziky odvodil Max Planck tvar spektra absolútne čierneho telesa, t.j. Planckov zákon vyžarovania pre spektrálnu hustotu intenzity vyžarovania v dutine absolútne čierneho telesa nasledovným postupom:
· zvážil, že predpoklady z ktorých vychádzali Rayleigh a Jeans pri odvodzovaní spektrálnej hustoty intenzity Ml (l,T) dl v jednotkovom objeme dutiny v intervale vlnových dĺžok l al + dl boli správne až po určenie skutočného počtu stojatých vĺn v dutine. Usúdil, že I. a II. veta termodynamická platí i pre javy spojené s elektromagnetickým žiarením;
· na základe kvantovej hypotézy, prisúdil mikrooscilátoru (kmitajúcemu atómu) v stene absolútne čierneho telesa energie určené vzťahom
En = n e , (1)
![]() = h f , (2)
= h f , (2)
kde n je celé číslo a n = 1, 2, 3, .... a kde f je frekvencia oscilácií atómov a h Planckova konštanta
· na základe predchádzajúceho predpokladu vyjadril spektrálnu hustotu intenzity Ml (l,T) dl vzťahom
Ml (l,T) dl = ![]() n (l) dl , (3)
n (l) dl , (3)
kde skutočný počet stojatých vĺn n v dutine je určený (pozri odvodenie v hypertexte Rayleighov- Jeansov zákon - vzťah (2)
![]() . (4)
. (4)
Vypočítajme strednú hodnotu energie ![]() oscilátora s kvantovanými hodnotami energie, určenými vzťahom (1). Podľa štatistickej fyziky sústava, ktorá je v termodynamickej rovnováhe s okolím, sa s pravdepodobnosťou
oscilátora s kvantovanými hodnotami energie, určenými vzťahom (1). Podľa štatistickej fyziky sústava, ktorá je v termodynamickej rovnováhe s okolím, sa s pravdepodobnosťou
![]() , (5)
, (5)
nachádza v stave s energiou E. Vo vzorci (5) k je Boltzmannova konštanta, c je normovací faktor, ktorý musíme zvoliť tak, aby
![]() (6)
(6)
Ak sa sústava môže nachádzať v určitých diskrétnych stavoch s energiami En , potom pravdepodobnosť toho, že sústava sa bude nachádzať práve v stave s energiou En , bude
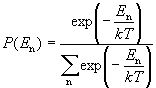 , (7)
, (7)
kde v menovateli sčítame cez všetky n. Stredná hodnota energie pri (absolútnej) teplote T je daná vzťahom
![]() . (8)
. (8)
Ak dosadíme (5), (1) a (2) do rovnice (8), dostaneme
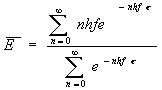 , (9)
, (9)
kde t = 1/ kT. Pravú stranu rovnice (9) možno prepísať ako
![]() . (10)
. (10)
Súčet nekonečného radu v (10) nájdeme, ak si uvedomíme, že ide o nekonečný geometrický rad, pre ktorý platí:
![]()
Na základe toho dostaneme
![]() ,
,
odkiaľ po derivovaní vyplýva konečný výsledok pre strednú energiu kvantového oscilátora
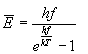 . (11)
. (11)
Výsledný vzorec pre spektrálnu hustotu intenzity vyžarovania v dutine získame po dosadení vzťahu (11) do rovnice (3), s uvážením, že platia nasledovné vzťahy:
Ml (l,T) dl = - Ml ( f ,T) df ,
![]()
Po dosadení
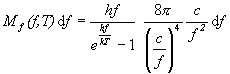 ,
,
a vykrátení dostaneme Planckov zákon vyžarovania v tvare
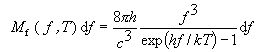 .
.
Možno ukázať, že pre malé frekvencie , alebo vysoké teploty z Planckovho zákona vyplýva platnosť Rayleighovho- Jeansovho zákona.