 Príklady
Príklady
1. Pri prechode Zeme aféliom je Zem o 3,3 % ďalej od Slnka ako v perihéliu. Určte o koľko by bola teplota Zeme v aféliu menšia ako v perihéliu. Zem považujeme za čierne teleso, ktorého stredná teplota v perihéliu je 15 0C. [ Dt = 4,6 0C]
2. Žiarenie Slnka je svojim spektrálnym zložením podobné žiareniu absolútne čierneho telesa s maximom na vlnovej dĺžke 480 nm. Určite teplotu povrchu Slnka, výkon vyžarovania a hmotnosť, ktorú Slnko stráca za každú sekundu v dôsledku tohto žiarenia. Odhadnite dobu, za ktorú sa hmotnosť Slnka týmto spôsobom zmenší o 1%. ( Polomer Slnka je R=6,96.105 km, hmotnosť Slnka je mS = 1,99 1030 kg). [ T = 6033 K, Dm = 5.109 kg.s-1 t = 3,9.1018 s t = 1,2.1011 rokov]
3. Vodnú paru teploty 100 0C vedieme potrubím dĺžky 3,5 m s vonkajším priemerom 3,75 cm. Celkové straty tepla do okolia sú E = 1 161 kJ za hodinu. Koľko percent strát pripadá na tepelné žiarenie, ak koeficient absorpcie materiálu potrubia k = 0,5? Teplota okolia sa udržiava na konštantnej hodnote 24 0C. [ Wz/Wrel = 42 % ]
4. Na ten istý kov dopadne svetlo s frekvenciou f a následne svetlo s frekvenciou o tretinu menšou ako bolo pôvodné. Určite, v ktorom prípade budú mať vzniknuté fotoelekróny väčšiu kinetickú energiu. [ V prvom.]
5. Na ten istý kov dopadne svetlo s frekvenciou f a následne svetlo s frekvenciou o tretinu menšou ako bolo pôvodné. Určite o koľko sa zmení kinetická energia oproti fotoelektónom, vzniknutých pri prvom ožiarení. [Ek1- Ek2 = Ek1/3]
6. Výstupná práca dvoch materiálov je v pomere 2:1. Určite v akom pomere budú kinetické energie fotoelektrónov, ak v druhom prípade frekvencia poklesne na polovicu hodnoty frekvencie prvého žiarenia. [Ek1/ Ek2= 2].
7. Výstupná práca striebra je 4,28 eV, hliníka 3,74 eV, zlata 4,58 eV, bárya 2,29 eV , draslíka 2,15 eV a lítia 2,39 eV, cézia 1,89eV. Pri výrobe fotočlánku pre viditeľnú oblasť, ktorý materiál by ste vybrali ako najvhodnejší? Svoju odpoveď zdôvodnite.
8. Od okolia izolovaná zlatá guľôčka s polomerom R = 1 cm je ožiarená svetlom vlnovej dĺžky l0 = 200 nm. Vypočítajte a) na aký maximálny potenciál Vbm sa nabije guľôčka v dôsledku straty fotoelektrónov, b) aký náboj vznikne na nej, c) koľko elektrónov sa uvoľnilo? [ N= 5,56. 106 ]
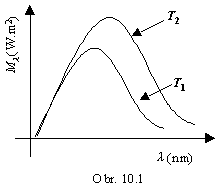
9. Študent na skúške z fyziky nakreslil dve krivky (pozri obr. 10.1) odpovedajúce spektrálnej hustote intenzity vyžarovania absolútne čierneho telesa pre dve rôzne teploty (T2>T1). Získa za odpoveď plný počet bodov?
10. Teleso zohriaté na teplotu T1 = 2500 K postupne chladne. Vlnová dĺžka svetla, na ktorú pripadá relatívne najviac energie v spektre žiarenia tohto telesa sa zmení o Dl = 0,8 mm. Vypočítajte, na akú teplotu T2 sa teleso ochladilo za predpokladu, že žiari ako absolútne čierne teleso. [T2 = 1 479,6 K ]
11. Nájdite výsledok pôsobenia operátorov (d2/dx2)x2 na funkciu ex . [ex(2+4x+x2)]
12. Nájdite výsledok pôsobenia operátora [(d/dx)x ]2 na funkciu cos x.. [(cos x – x sin x)2]
13. Nájdite výsledok pôsobenia operátora [(d/dx)x ]2 na funkciu ex. [e2x(1+x)2]
14. V algebre operátorov záleží na ich poradí. Dva operátory komutujú ak spĺňajú podmienku ![]() .
.
15. Pôsobením operátorov na diferencovateľnú funkciu y(x) dokážte platnosť nasledovných komutačných relácií ![]() .
.
16. Dokážte, že operátory ![]() sú nekomutatívne.
sú nekomutatívne.
17. Dokážte, že operátory ![]() vzájomne komutujú. [v = 10 m·s–1]
vzájomne komutujú. [v = 10 m·s–1]
18. Ukážte, že vlnová funkcia y(x,t) = A ![]() je vlastnou funkciou operátora hybnosti
je vlastnou funkciou operátora hybnosti ![]() a nájdite príslušnú vlastnú hodnotu tohto operátora! [ Pozri definíciu , p]
a nájdite príslušnú vlastnú hodnotu tohto operátora! [ Pozri definíciu , p]
19. Aká je grupová rýchlosť voľnej mikročastice pohybujúcej sa rýchlosťou mnohonásobne menšou, ako je rýchlosť svetla? Predpokladajte pri tom, že závislosť celkovej energie mikročastice od hybnosti vyjadruje rovnica E= p2/2m0. [ vg = v]
20. Odhadnite šírku čiary Dl a rozptyl frekvencie Dn pre svetelný impulz rubínového lasera, ktorého doba trvania je t = 1 ns a vlnová dĺžka l = 630 nm. [ Dl ³ l2/(4pcDt) ³0,105 pm, D f ³7,96 .107 s]
21. Častica hmotnosti m v jednorozmernom potenciálnom poli má celkovú energiu rovnú![]()
(w - uhlová frekvencia harmonického oscilátora). Pomocou Heisenbergových vzťahov neurčitosti vypočítajte najmenšiu možnú energiu častice v tomto poli! [ E = hw/ 4p]
22. Akú rýchlosť v dosiahne fotónová raketa s hmotnosťou m = 10 t, keď jej svetelný zdroj vlnovej dĺžky l = 500 nm pracuje s výkonom P = 1 MW a je zapnutý 365 dní? Koľko fotónov sa pri tom vyžiari za jednu sekundu?
23. Poloha elektrónu je určená s presnosťou Dx = 10–10 m. Vypočítajte neurčitosť jeho hybnosti Dpx. Predpokladajme, že energia elektrónu je rádovo E ≈ 1 keV. Vypočítajte percentuálnu neurčitosť jeho energie! [Dp >³5,27 10-25 kg.m-s-1, DE/E .100= 6.18 %]
24. Strela s hmotnosťou ms = 0,05 kg a elektrón s hmotnosťou me = 9,11×10–31 kg majú rovnakú rýchlosť v = 300 m×s–1, ktorá bola určená s presnosťou 0,01%. Aká je nepresnosť v určení ich polohy, keď poloha bola určovaná súčasne s rýchlosťou? [Pre strelu (Dx)s ³ h/4p mev =3,52.10-32 m×s–1, Pre elektrón (Dx)e ³ h/4p mev =1,93.10-3]
25. Použitím vzťahov neurčitosti odhadnite minimálnu energiu, ktorú môže mať častica s hmotnosťou m, nachádzajúca sa v nekonečne hlbokej jednorozmernej potenciálovej jame šírky a. ![]()
26. Doba života excitovaného stavu jadra je Dt = 10–12 s. Aká je neurčitosť Dl vo vlnovej dĺžke emitovaného fotónu žiarenia g, keď jeho energia je E = 1,6 MeV? [![]() m]
m]
27. Vypočítajte neurčitosť rýchlosti elektrónu v atóme, keď neurčitosť jeho polohy je aspoň 10 pm (rozmery atómu sú cca 0,1 nm.). [![]() m×s–1]
m×s–1]
28. S akou presnosťou Dx možno lokalizovať fotón s vlnovou dĺžkou 550 nm na svojej dráhe, keď čas vyžiarenia fotónu atómom je t = 10 ns (pre neurčitosť doby vyžiarenia predpokladajte Dt = t/2)? Aká je relatívna presnosť určenia vlnovej dĺžky (Dl/l)? ![]()
29. Pomocou Heisenbergových vzťahov neurčitosti vypočítajte rozmer jadra, keď energia protónu v atómovom jadre je E = 10 MeV. ![]()
30. Priraďte de Broglieho vlnovú dĺžku zrnku peľu s hmotnosťou m = 0,05 mg. [3,3 .10-34 m]
31. Priraďte de Broglieho vlnovú dĺžku častici s hmotnosťou m = 100 g, pohybujúcej sa priamočiaro rýchlosťou 20 ms-1. [3,3 .10-34 m]
32. Určite koľkokrát je väčšia vlnová dĺžka elektrónu s kinetickou energiou 1 MeV s vlnovou dĺžkou fotónu s energiou 1 MeV. [18,75]
33. Rozlišovacia schopnosť mikroskopu je limitovaná použitou vlnovou dĺžkou, t.j. z principiálnych dôvodov nemôžu byť rozlíšené detaily, ktoré sú menšie ako použitá vlnová dĺžka. Predpokladajme, že chceme „vidieť“ do vnútra atómu a rozlíšiť detaily rozmerov 10-11 m. Akú energiu elektrónov, resp. fotónov by bolo treba použiť na tento účel. [Wke = 2,41.10-15 J = 1,5.104 eV ; Wkf = 19,9.10-15 J = 12,4.104 eV]
34. Je možné bežným optickým mikroskopom dosiahnuť rozlíšenie detailov rozmerov 10-11 m? Svoju odpoveď zdôvodnite.
35. Aká je frekvencia, energia a hybnosť fotónu s vlnovou dĺžkou 500 nm, keď jeho zotrvačná hmotnosť m = 4,42×10–36 kg?[![]() Hz,
Hz, ![]() J,
J, ![]() kg×m×s–1]
kg×m×s–1]
36. Vypočítajte maximálnu frekvenciu fotónu a jeho vlnovú dĺžku! Predpokladajte, že fotón môže byť vyžiarený po okamžitom zastavení elektrónu s kinetickou energiou Ek = 100 eV. [ ![]() s–1,
s–1, ![]() nm ]
nm ]
37. Akou rýchlosťou sa musí pohybovať elektrón, aby sa jeho kinetická energia rovnala energii fotónu s vlnovou dĺžkou l1 = 400 nm, resp. l2 = 700 nm? [ ![]() (pre 400 nm
(pre 400 nm ![]() m×s–1 a 700 nm
m×s–1 a 700 nm ![]() m×s–1), kde m0 je pokojová hmotnosť elektrónu. ]
m×s–1), kde m0 je pokojová hmotnosť elektrónu. ]
38. Vypočítajte vlnovú dĺžku de Broglieho vlny odpovedajúcej elektrónu s kinetickou energiou Ek = 1 MeV! [ ![]() pm ]
pm ]
39. Koľko fotónov vyžaruje za jednu sekundu zdroj monochromatického elektromagnetického žiarenia s vlnovou dĺžkou l = 0,6 mm, keď jeho výkon P je rovný 60 W? [ N = Plt / hc = 1,81 .1020 ]
40. Výkon žiarivky je P = 5 W. Vypočítajte počet fotónov N so strednou vlnovou dĺžkou l = 350 nm, dopadajúcich za 1 s na 1 m2 plochy v rovnorodom prostredí vo vzdialenosti 1 km od zdroja svetla. [ N = Pl / 4p l2 hc = 7,0 .1011 ]
41. Záporne nabitá častica urýchlená potenciálovým rozdielom DU = 206 V má de Broglieho vlnovú dĺžku l = 2 pm. Nájdite hmotnosť tejto častice, ak je známe, že jej náboj sa rovná elementárnemu náboju elektrónu. [ m = h2 / (2l2 e DU)]
